個性と行動シンドロームの統計解析

趣旨

個性や行動シンドローム、個性と適応度の関連を調べるうえで、統計解析の部分で勉強したことをまとめていきます。個性や行動シンドロームの概念的な部分は日本生態学会誌に総説 を書いていますのでそちらを参照ください。

自分で分析を始めたら、その時に詰まったところなどまとめていきます。

個体内で反復測定をしたデータ分析に共通の手法ですので、個性だけでなく、成長過程での形質相関の変化など色々応用できると思います。

Rコードは右上 “Code” ボタン → “Download Rmd” でダウンロードできます。

---

General settings

rm(list=ls())  # reset workspace
options(scipen=100)  # do not show numbers using exponential

# install & load packages
pacman::p_load(
  tidyverse
  # , openxlsx # open excel
  , magrittr   # extended pipe
  # , foreach    # Parallel processing
  , knitr  
  , kableExtra # nice tables
  , pander     # nice tables
  # , svglite    # Export SVG plots
  # , patchwork   # combine multiple plots
)

# Rmarkdown settings
knitr::opts_chunk$set(
  prompt  = FALSE,  # Do not add > or + in inline-code
  message = FALSE, 
  comment = "", 
  warning = FALSE,  # Mute warnings
  tidy    = TRUE
  ) 
options(knitr.kable.NA = '') # Hide NAs in kable table

---

MCMCglmm : Houslay & Wilson 2017 Behav Ecol

T.M. Houslay & A.J. Wilson, Behavioral Ecology 2017: Supplement のまとめ。

問題点であるBLUPとは

Best Linear Unbiased Predictors - 混合モデルで推定された、ランダム効果の各個体での推定値 - 当然大きな誤差が伴う

【問題となっている手法】
個体IDにランダム効果を当てた混合モデルにおいて、各個体のランダム効果値（BLUP, 各個体の行動性向を示す）を抽出し、それを用いてさらに分析を進める（行動シンドロームなど）

【問題点】
点推定であるBLUPには誤差が反映されないので、BLUPを使った分析では慌て者の過誤が起こりやすくなる（編集元のSupplementではBLUPによる分析もしているがここでは省略）

【解決策】
個性分析（行動Repeatability）と追加分析（行動シンドロームや個性ー適応度の関連）を一つの混合モデルで片付けてしまう

---

Install & load packages

pacman::p_load(
  MCMCglmm
  , lme4
  , broom.mixed # create tidy output of glmm result
  , nadiv
  , coda # Judge MCMC convergence
  )

# Supplementで用意されている仮想データ
df_syndrome <- read_csv("learn_Personality_stats_dat_syndrome.csv")

---

Data assumption

ここでは、複数の繰り返し計測した行動指標と、一回計測の適応度形質（mating success）データを想定。

今回の仮想データは全てオスのもので、以下の列を持つ

• Individual ID
• The repeat number for each behavioural test, assay_rep
• boldness, measured 4 times per individual
• exploration, measured 4 times per individual
• fitness, a single value for each individual
• Individual body_size, as measured on the day of testing.

---

単回帰モデル

• 各行動形質での、個体差による表現型分散の割合を計算

• lme4にて

• 計測の反復IDは固定効果に

• 個体IDがrandom effects

• 計測可能な個体の状態（ここでは体サイズ）はScaling or Centringして固定効果に

• 行動シンドロームを調べる全形質でこれを行う

lmer_b <- lmer(
  boldness ~ scale(assay_rep, scale=FALSE) + scale(body_size) + 
    # Don't forget scaling variables!
    (1|ID),
  data = df_syndrome
  )

plot(lmer_b)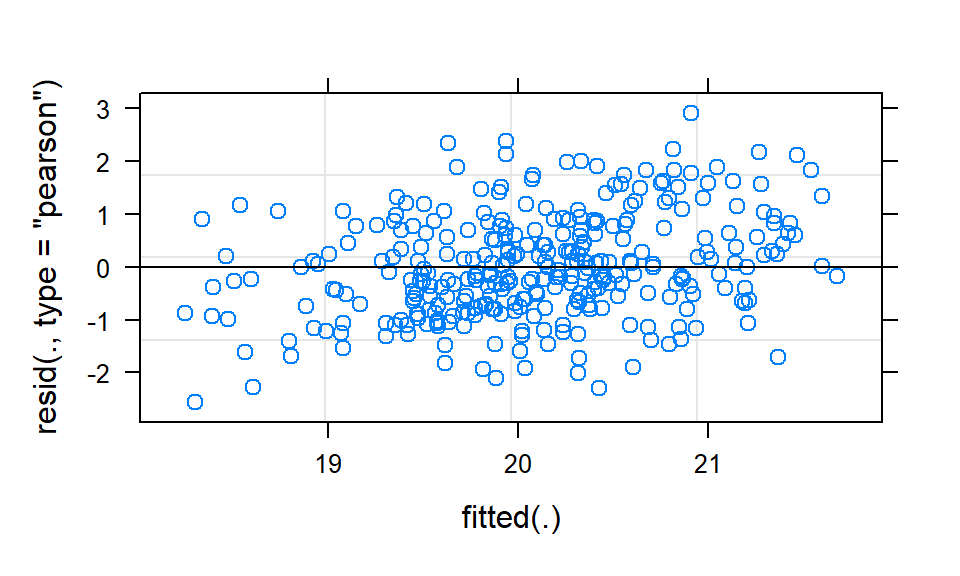

qqnorm(residuals(lmer_b))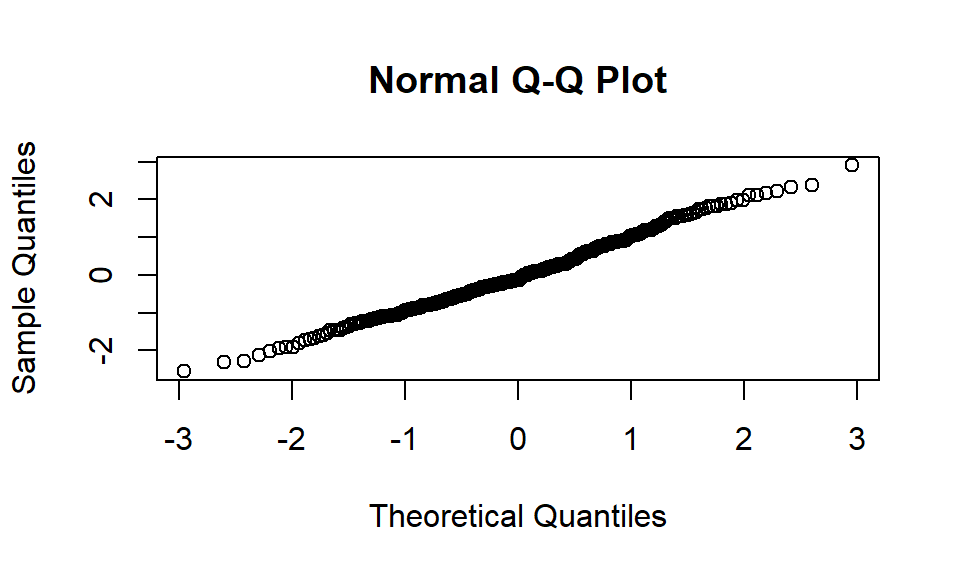

hist(residuals(lmer_b))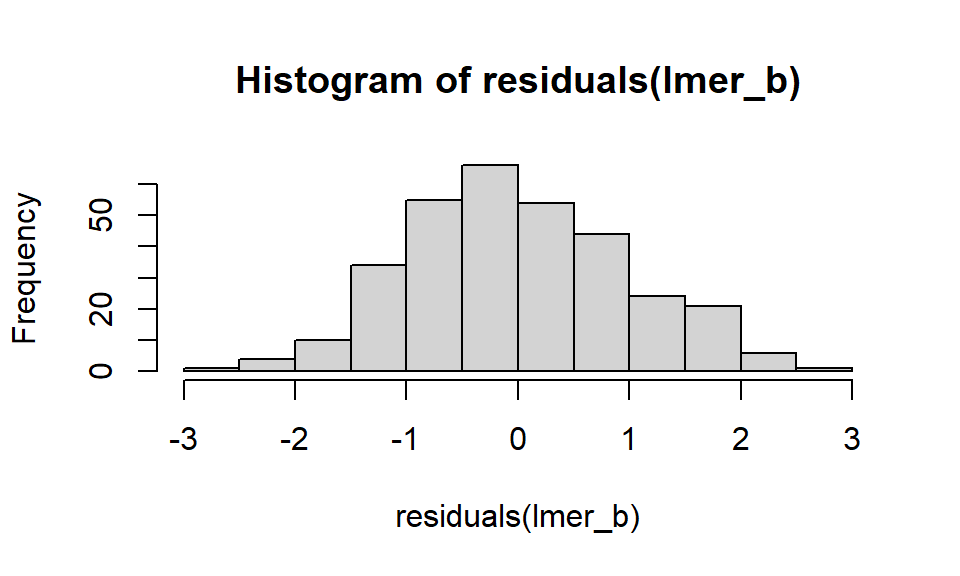

summary(lmer_b)

Linear mixed model fit by REML ['lmerMod']
Formula: boldness ~ scale(assay_rep, scale = FALSE) + scale(body_size) +  
    (1 | ID)
   Data: df_syndrome

REML criterion at convergence: 1061.4

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-2.3666 -0.6478 -0.1155  0.6445  2.6892 

Random effects:
 Groups   Name        Variance Std.Dev.
 ID       (Intercept) 0.6951   0.8337  
 Residual             1.1681   1.0808  
Number of obs: 320, groups:  ID, 80

Fixed effects:
                                Estimate Std. Error t value
(Intercept)                     20.09134    0.11108 180.871
scale(assay_rep, scale = FALSE) -0.04813    0.05404  -0.891
scale(body_size)                 0.14113    0.10893   1.296

Correlation of Fixed Effects:
            (Intr) s(_s=F
s(_,s=FALSE  0.000       
scl(bdy_sz)  0.000 -0.002

• ここではrandom effectsのvariance componentに興味がある。

• 動物の個性の証拠となるのは、repeatability (= intraclass correlation coefficient)

• Repeatability:

  • \(\frac{個体差による分散}{固定効果を考慮したうえでの全分散} = \frac{V_{ID}}{V_{ID} + V_{residual}}\)

broom.mixed::tidy(lmer_b, effects = "ran_pars", scales = "vcov") %>%
  select(group, estimate) %>%
  spread(group, estimate) %>%
  mutate(Repeatability = ID/(ID + Residual)) %>% 
  kable("html", digits = 3) %>% 
  kable_styling("striped", position = "left")  

ID	Residual	Repeatability
0.695	1.168	0.373

この仮想データでは、ばらつきの37%が固定効果ではなく個体差によるもの。

---

行動シンドローム：Bivariate models

• MCMCglmmでの、行動2形質を応答変数に置いたモデルを組む。

• 各行動形質とそれらの共分散に対する、個体間分散を推定

事前分布の設定

解説は以下参照

• Coding hub

• Course notes

• カテゴリカル変数にはGelman priorを当てはめる

• 複数の事前分布に対し結果が頑健か見ておくと良い

固定効果にはNormal distribution、(co)variancesにはinverse Wishartを事前分布として使っている。

---

指定するもの

• B: 固定効果の事前分布。Defaultは信仰の弱い正規分布

• R: 残差

• G: ランダム効果

• ランダム効果の数だけ指定。例：

    G = list(
      G1 = list(V = 1, nu = 1, alpha.mu = 0, alpha.V = 1000),
      G2 = list(V = 1, nu = 1, alpha.mu = 0, alpha.V = 1000),
      )
    )

• alpha.mu: Prior mean

• alpha.V: 分散行列

---

inverse Wishart事前分布の変数

• V: 事前分布のピークを決める。よく使われるのは1

• nu: 信仰の強さ＝分布の偏り を決める。よく使われるのは0.002

prior_E_B_1px = list(
  R = list(V = diag(2), nu = 0.002),
  G = list(
    G1 = list(
      V = diag(2), 
      nu = 2, 
      alpha.mu = rep(0,2), 
      alpha.V = diag(25^2,2,2))
    )
  )

---

MCMCglmmモデル

全体のコード

MCMCglmm(
  # Response variables. Combine after scaling
  cbind(scale(exploration), scale(boldness)) ~ 
    trait-1 +
    trait:scale(assay_rep, scale = FALSE) +
    trait:scale(body_size),
  random =~ us(trait):ID,
  rcov =~ us(trait):units,
  family = c("gaussian","gaussian"),
  prior = prior_E_B_1px,
  nitt = 150000,
  burnin = 10000,
  thin = 30,
  verbose = TRUE,
  data = as.data.frame(df_syndrome)
  )

項目ごとの解説

• Response variable: cbind after scaling

  cbind(scale(exploration), scale(boldness)) ~ 

• Predictor variable:

  • 各形質に対し切片を用意

    trait-1 +

• trait keywordにより多変量モデルであることを明記
• 固定効果による形質への影響を、それぞれの形質で推定

    trait:scale(assay_rep, scale = FALSE) +
    trait:scale(body_size),

• Random effects structureを設定
  

  • ‘unstructured’ (us) 共分散行列を個体IDに適用
    以下を計算するため

    • 個体差による、それぞれの行動形質の分散
    • これらの分散の共分散

  random =~ us(trait):ID,

• 残差分散の構造を設定

  • ‘within-individual variation’
  • 各個体で反復計測しているので、ここでもunstructured covariance matrixを設定
    • 各形質での残差分散と共分散を計算

    rcov =~ us(trait):units,

• MCMCプロセスの設定
  収束が悪い時はこれらの値を大きく上げる
  • 反復試行数 (Iterations) nitt
    収束が悪ければ青天井
  • 不安定な初期のIterationを切り捨てる数burnin
    収束が悪ければ50000など
  • 使うIteration間隔 thin: Samplingでの自己相関を減らす
    収束が悪ければ200など

    nitt=420000,
    burnin=20000,
    thin=100,

• データセット
  • MCMCglmmではtbl_dfを受け入れないのでas.data.frame

    data = as.data.frame(df_syndrome)

---

MCMCの収束

Traceは一定の傾向を持っていてはいけないー未収束を示す。ある値の上下で終始ギザギザしていると収束が示唆。

ランダム効果のMCMC連鎖

mcmc_E_B_us <- readRDS("learn_Personality_stats_mcmc_syndrome.obj")
plot(mcmc_E_B_us$VCV)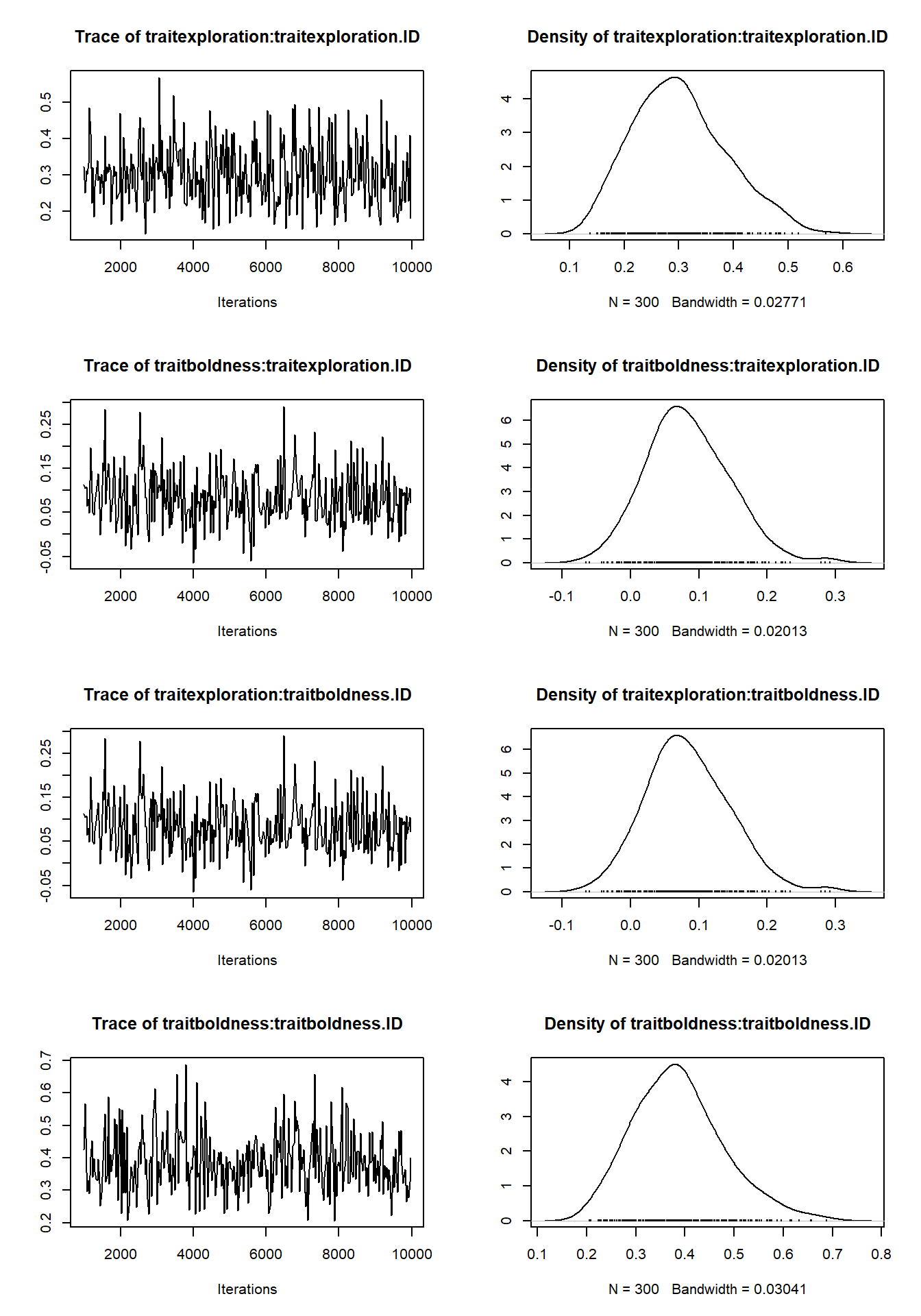

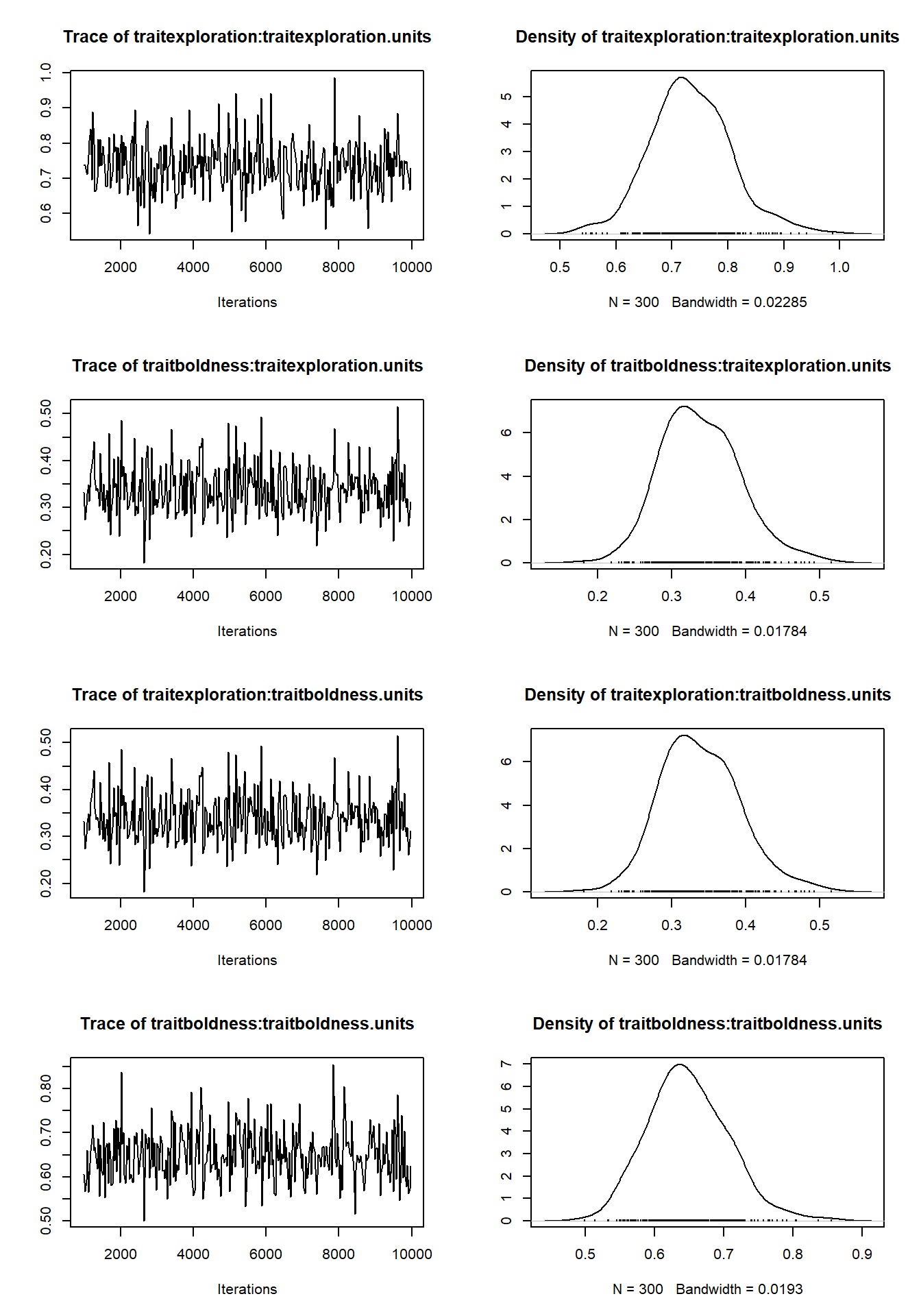
固定効果の収束過程

plot(mcmc_E_B_us$Sol)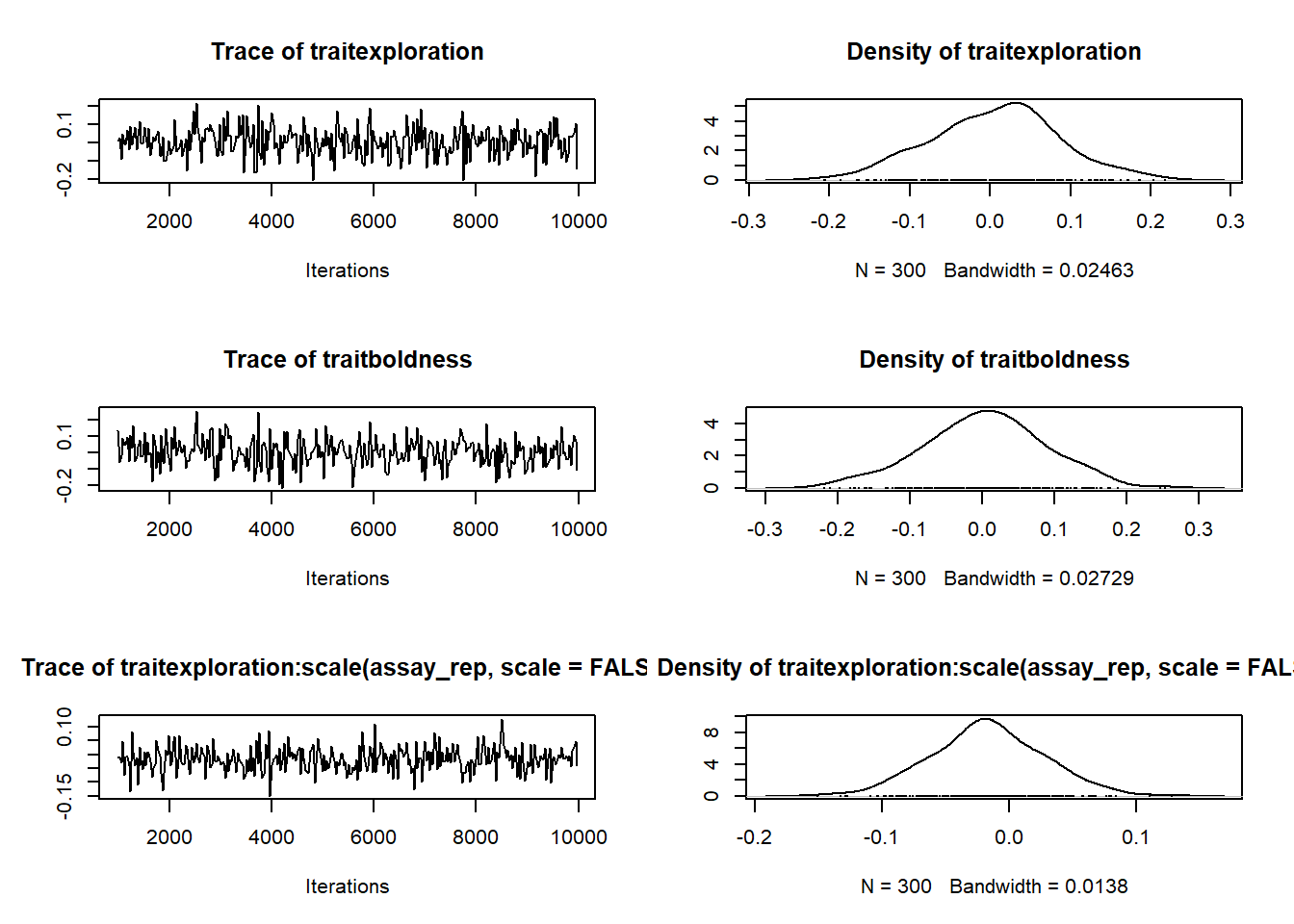

---

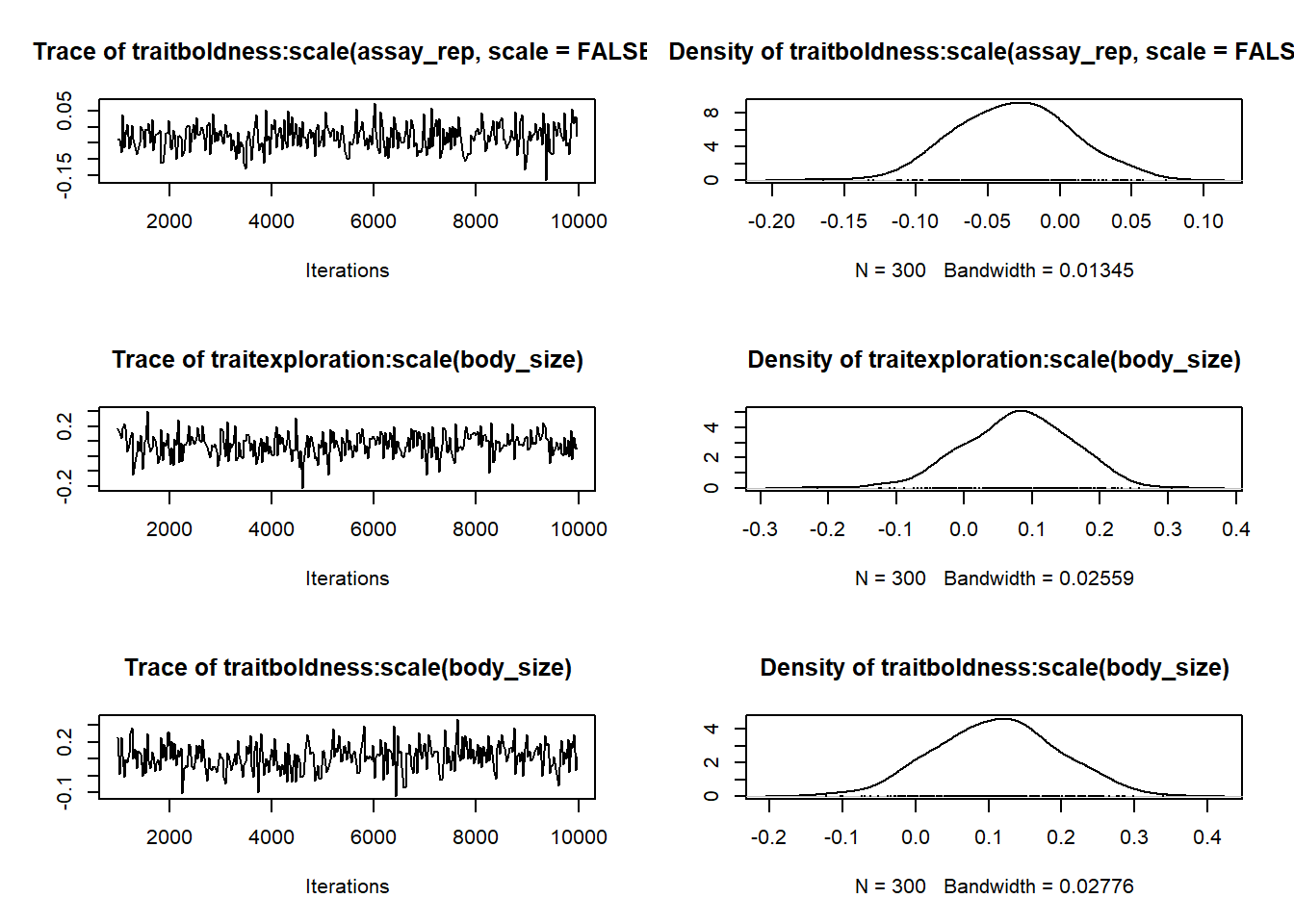
geweke.diag

• Markov連鎖の初期と後期での平均値が同じか調べる
  • 初期設定では、初期10%と後期50%
• もし連鎖がstationary distributionに達していれば、
  • 二つの平均は同じ
  • Geweke統計量はasymptotically standard normal distribution
• test statistic: Z-score
  • \(\frac{Sample\ meansの差}{推定standard\ error}\)
  • SEは、spectral density at zeroから推定
    • 自己相関が考慮に入っている
  • calculated under the assumption that the two parts of the chain are asymptotically independent, which requires that the sum of frac1 and frac2 be strictly less than 1

geweke.diag(mcmc_E_B_us$Sol, frac1=0.1, frac2=0.5)

Fraction in 1st window = 0.1
Fraction in 2nd window = 0.5 

                                traitexploration 
                                         1.60470 
                                   traitboldness 
                                         1.68896 
traitexploration:scale(assay_rep, scale = FALSE) 
                                        -0.95071 
   traitboldness:scale(assay_rep, scale = FALSE) 
                                        -0.83522 
               traitexploration:scale(body_size) 
                                         0.00896 
                  traitboldness:scale(body_size) 
                                        -0.26172 

Z値が０からほど遠いので、このMarchov連鎖は収束していないとみるべき

---

モデルが2つ以上あるときにはgelman.diagによる判定もできる

gelman.diag(mcmc.list(m1$Sol, m2$Sol))

Repeatability

反復性を計算するために、新たに ‘個体差で説明された行動形質ばらつきの割合’ の事後分布を作る

• SummaryにあるVariance componentsの名前に基づいて計算

• ここではExplorationが対象

mcmc_prop_E <- mcmc_E_B_us$VCV[,"traitexploration:traitexploration.ID"]/
  (mcmc_E_B_us$VCV[,"traitexploration:traitexploration.ID"] +
     mcmc_E_B_us$VCV[,"traitexploration:traitexploration.units"])

plot(mcmc_prop_E)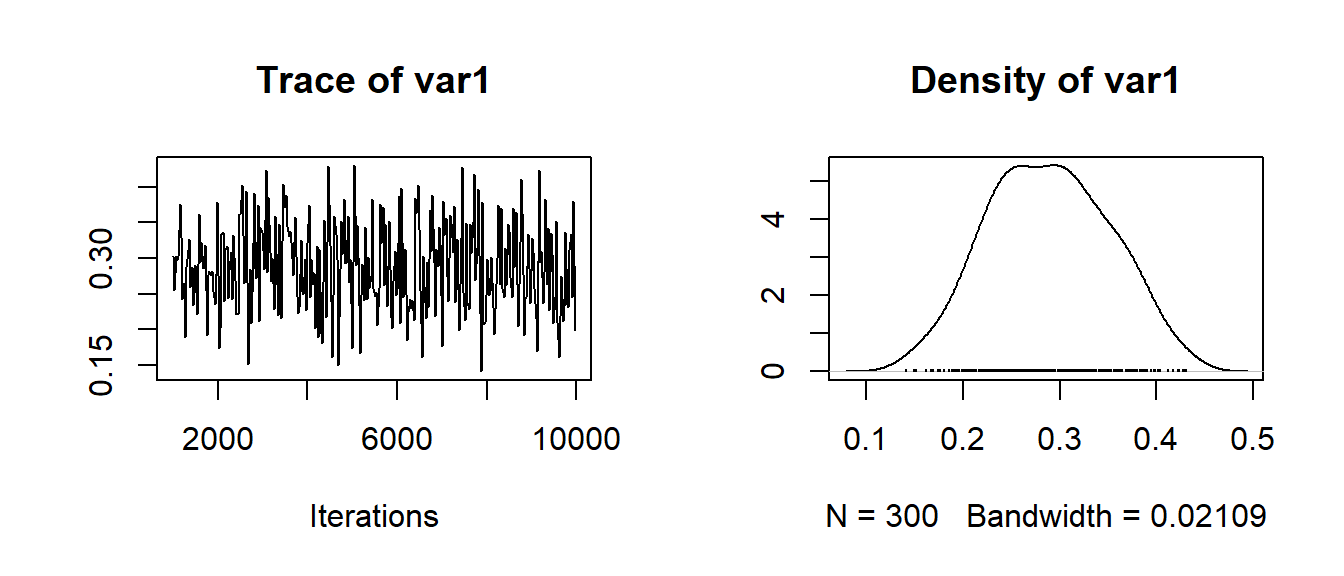

mean(mcmc_prop_E)

[1] 0.2887684

# 95% CIs
HPDinterval(mcmc_prop_E)

         lower     upper
var1 0.1691948 0.4039535
attr(,"Probability")
[1] 0.95

Bayesian 95%信頼区間が０を跨がないことが古典的（頻度主義的）な統計的有意を示すだと言われるが、ここで扱っているvariance componentsは、MCMCglmmでは必ず正の値をとる

• 信頼区間が０を跨がない≠有意
• 下限が０に近ければ、Repeatabilityが弱いと考えるべき

なお、Variance componentsの名前は以下で調べられる

mcmc_E_B_us$VCV %>% 
  as.tibble() %>% 
  colnames()

[1] "traitexploration:traitexploration.ID"   
[2] "traitboldness:traitexploration.ID"      
[3] "traitexploration:traitboldness.ID"      
[4] "traitboldness:traitboldness.ID"         
[5] "traitexploration:traitexploration.units"
[6] "traitboldness:traitexploration.units"   
[7] "traitexploration:traitboldness.units"   
[8] "traitboldness:traitboldness.units"      

• 個体差による分散は
  trait{*trait name*}:trait{trait name}.ID
• 残差分散は
  trait{trait name}:trait{trait name}.units

---

Covariance

Repeatabilityの計算プロセスを共分散に応用できる。

個体間での形質間相関の事後分布：

• \(\frac{形質間の共分散}{各形質の分散の平方根を掛け合わせたもの}\)

  • 共分散を-1~1にスケーリング

mcmc_cor_EB <- mcmc_E_B_us$VCV[,"traitboldness:traitexploration.ID"]/
  (sqrt(mcmc_E_B_us$VCV[,"traitboldness:traitboldness.ID"])*
     sqrt(mcmc_E_B_us$VCV[,"traitexploration:traitexploration.ID"]))

plot(mcmc_cor_EB)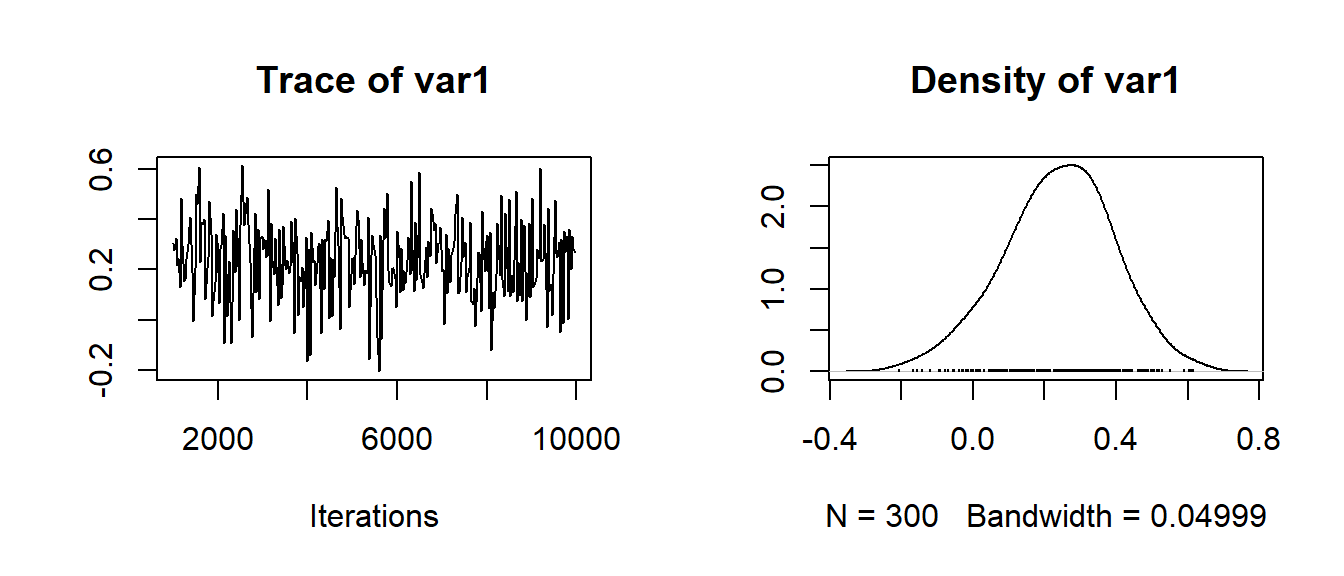

mean(mcmc_cor_EB)

[1] 0.238657

HPDinterval(mcmc_cor_EB)

           lower     upper
var1 -0.06996265 0.5195749
attr(,"Probability")
[1] 0.95

相関は正負どちらもとりうるので、95%信頼区間が０を跨ぐかは頻度主義的な統計的有意を示す。ここでは信頼区間が０を跨いでいるので、有意な行動シンドロームはないと結論付ける。

---

さらに形質を加える

仮想データセットでの、行動２形質（反復測定）と適応度（1回計測）の関係を調べる。

# 相対適応度を算出し、rel_fitnessに格納
df_syndrome %<>%
  mutate(rel_fitness = fitness/mean(fitness, na.rm=TRUE))

---

事前分布を設定

注意

• 1回計測の形質（ここでは適応度）では、残差分散（個体内分散）は０
• 1回計測の計測との間のすべての個体内形質相関も０
  • fixでVariance componentを特定の値に固定
    • 分散は正の値でないといけないので、個体内分散を小さな正の値で代入（ここでは0.0001）
    • 個体内分散＝残差分散R

prior_E_B_fit_1px = list(
  R = list(
    # 反復測定形質が2つの後に1回計測形質の分散を指定するので、3つ目の要素に0.0001を代入
    V = diag(c(1,1,0.0001),3,3), 
    nu = 1.002, 
    # 3つ目のVariance component = 1回計測形質を固定
    fix = 3
    ),
  G = list(
    G1 = list(
      V = diag(3), nu = 3, alpha.mu = rep(0,3), alpha.V = diag(25^2,3,3)
      )
    )
  )

---

MCMCglmmモデル

全体のコード

mcmc_E_B_fit <- MCMCglmm(
  cbind(scale(exploration), scale(boldness), rel_fitness) ~ 
    trait-1 + 
    at.level(trait,1):scale(assay_rep, scale = FALSE) +
    at.level(trait,2):scale(assay_rep, scale = FALSE) +
    trait:scale(body_size),
  random =~ us(trait):ID,
  rcov =~ us(trait):units,
  family = c("gaussian","gaussian","gaussian"),
  prior = prior_E_B_fit_1px,
  nitt = 100000,
  burnin = 10000,
  thin = 100,
  verbose = TRUE,
  pr = TRUE,
  data = as.data.frame(df_syndrome)
  )
# saveRDS(mcmc_E_B_fit, "learn_Personality_stats_mcmc_fit.obj")

個別解説

    at.level(trait,1):scale(assay_rep, scale = FALSE) +
    at.level(trait,2):scale(assay_rep, scale = FALSE) +

• at.level
  • specify that fixed effects are estimated only for certain traits
    • ここでは、反復計測assay_repの影響を反復計測された形質に対してだけ調べている
    • 一方、繰り返し測った体サイズの影響は全ての形質に対して調べている

  pr = TRUE,

• 各個体でのランダム効果（ID）の事後分布を保存
  • REMLでのBLUPに相当
  • 後で可視化
  • めっちゃファイルサイズデカくなる (もともと<1Mbのモデルでも、>8Mbになる)

---

結果

mcmc_E_B_fit <- readRDS("learn_Personality_stats_mcmc_fit.obj")

summary(mcmc_E_B_fit)

 Iterations = 10001:99901
 Thinning interval  = 100
 Sample size  = 900 

 DIC: 795.0887 

 G-structure:  ~us(trait):ID

                                     post.mean  l-95% CI u-95% CI eff.samp
traitexploration:traitexploration.ID   0.29540  0.148747  0.45910    900.0
traitboldness:traitexploration.ID      0.08595 -0.027963  0.20552    900.0
traitrel_fitness:traitexploration.ID   0.02778 -0.008056  0.06991    900.0
traitexploration:traitboldness.ID      0.08595 -0.027963  0.20552    900.0
traitboldness:traitboldness.ID         0.38911  0.231034  0.56482    900.0
traitrel_fitness:traitboldness.ID      0.09359  0.051660  0.13954   1009.0
traitexploration:traitrel_fitness.ID   0.02778 -0.008056  0.06991    900.0
traitboldness:traitrel_fitness.ID      0.09359  0.051660  0.13954   1009.0
traitrel_fitness:traitrel_fitness.ID   0.06048  0.042892  0.08079    289.6

 R-structure:  ~us(trait):units

                                        post.mean  l-95% CI u-95% CI eff.samp
traitexploration:traitexploration.units 0.7323518  0.604013 0.869493   900.00
traitboldness:traitexploration.units    0.3298602  0.226774 0.423178   900.00
traitrel_fitness:traitexploration.units 0.0005896 -0.006883 0.007051    81.69
traitexploration:traitboldness.units    0.3298602  0.226774 0.423178   900.00
traitboldness:traitboldness.units       0.6397129  0.529047 0.757717   900.00
traitrel_fitness:traitboldness.units    0.0014744 -0.005383 0.006489    66.25
traitexploration:traitrel_fitness.units 0.0005896 -0.006883 0.007051    81.69
traitboldness:traitrel_fitness.units    0.0014744 -0.005383 0.006489    66.25
traitrel_fitness:traitrel_fitness.units 0.0001000  0.000100 0.000100     0.00

 Location effects: cbind(scale(exploration), scale(boldness), rel_fitness) ~ trait - 1 + at.level(trait, 1):scale(assay_rep, scale = FALSE) + at.level(trait, 2):scale(assay_rep, scale = FALSE) + trait:scale(body_size) 

                                                    post.mean   l-95% CI
traitexploration                                    0.0001755 -0.1626782
traitboldness                                      -0.0051980 -0.1871777
traitrel_fitness                                    0.9976330  0.9396981
at.level(trait, 1):scale(assay_rep, scale = FALSE) -0.0203557 -0.0949575
scale(assay_rep, scale = FALSE):at.level(trait, 2) -0.0326581 -0.1050051
traitexploration:scale(body_size)                   0.0686491 -0.0822292
traitboldness:scale(body_size)                      0.0959950 -0.0546117
traitrel_fitness:scale(body_size)                   0.0092247 -0.0497545
                                                     u-95% CI eff.samp  pMCMC
traitexploration                                    0.1602554   900.00  0.973
traitboldness                                       0.1421898   900.00  0.936
traitrel_fitness                                    1.0548906   900.00 <0.001
at.level(trait, 1):scale(assay_rep, scale = FALSE)  0.0651687   767.60  0.642
scale(assay_rep, scale = FALSE):at.level(trait, 2)  0.0493624   900.00  0.451
traitexploration:scale(body_size)                   0.2049156   900.00  0.356
traitboldness:scale(body_size)                      0.2448215   414.66  0.236
traitrel_fitness:scale(body_size)                   0.0579210    98.24  0.760
                                                     
traitexploration                                     
traitboldness                                        
traitrel_fitness                                   **
at.level(trait, 1):scale(assay_rep, scale = FALSE)   
scale(assay_rep, scale = FALSE):at.level(trait, 2)   
traitexploration:scale(body_size)                    
traitboldness:scale(body_size)                       
traitrel_fitness:scale(body_size)                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• 個体内分散（~~.units）において、適応度（1回計測）が関わっているもの（rel_fitness:rel_fitness.units）は指定通り0.0001に固定され、effective sample sizeは0。

• 適応度（1回計測）が関わっている個体内の共分散はとても小さく、effective sample sizeも小さくなっているはず

行動シンドロームが以前のモデルと近い値になっているか確認

mcmc_E_B_fit_cor_EB <- mcmc_E_B_fit$VCV[,"traitboldness:traitexploration.ID"]/
  (sqrt(mcmc_E_B_fit$VCV[,"traitboldness:traitboldness.ID"])*
     sqrt(mcmc_E_B_fit$VCV[,"traitexploration:traitexploration.ID"]))

mean(mcmc_E_B_fit_cor_EB)

[1] 0.2455875

HPDinterval(mcmc_E_B_fit_cor_EB)

           lower     upper
var1 -0.06393585 0.5372623
attr(,"Probability")
[1] 0.95

適応度と行動形質の相関を抽出

mcmc_E_B_fit_cor_Efit <- mcmc_E_B_fit$VCV[,"traitrel_fitness:traitexploration.ID"]/
  (sqrt(mcmc_E_B_fit$VCV[,"traitrel_fitness:traitrel_fitness.ID"])*
     sqrt(mcmc_E_B_fit$VCV[,"traitexploration:traitexploration.ID"]))

mcmc_E_B_fit_cor_Bfit <- mcmc_E_B_fit$VCV[,"traitrel_fitness:traitboldness.ID"]/
  (sqrt(mcmc_E_B_fit$VCV[,"traitrel_fitness:traitrel_fitness.ID"])*
     sqrt(mcmc_E_B_fit$VCV[,"traitboldness:traitboldness.ID"]))

形質相関を図示

df_mcmc_cors <- data_frame(
  Traits = c(
    "Exploration, Boldness", "Exploration, Fitness", "Boldness, Fitness"
    ),
  Estimate = c(
    mean(mcmc_E_B_fit_cor_EB),
    mean(mcmc_E_B_fit_cor_Efit),
    mean(mcmc_E_B_fit_cor_Bfit)
    ),
  Lower = c(
    HPDinterval(mcmc_E_B_fit_cor_EB)[,"lower"],
    HPDinterval(mcmc_E_B_fit_cor_Efit)[,"lower"],
    HPDinterval(mcmc_E_B_fit_cor_Bfit)[,"lower"]
    ),
  Upper = c(
    HPDinterval(mcmc_E_B_fit_cor_EB)[,"upper"],
    HPDinterval(mcmc_E_B_fit_cor_Efit)[,"upper"],
    HPDinterval(mcmc_E_B_fit_cor_Bfit)[,"upper"]
    )
  )

ggplot(df_mcmc_cors, aes(x = Traits, y = Estimate)) +
  geom_pointrange(aes(ymin = Lower, ymax = Upper)) +
  geom_hline(yintercept = 0, linetype = "dotted") +
  scale_x_discrete(
    limits = c("Boldness, Fitness", "Exploration, Fitness", 
               "Exploration, Boldness")
    ) +
  labs(x = "Trait combinations",
       y = "Correlation (Estimate ±95% CIs)") +
  ylim(-1,1) +
  coord_flip()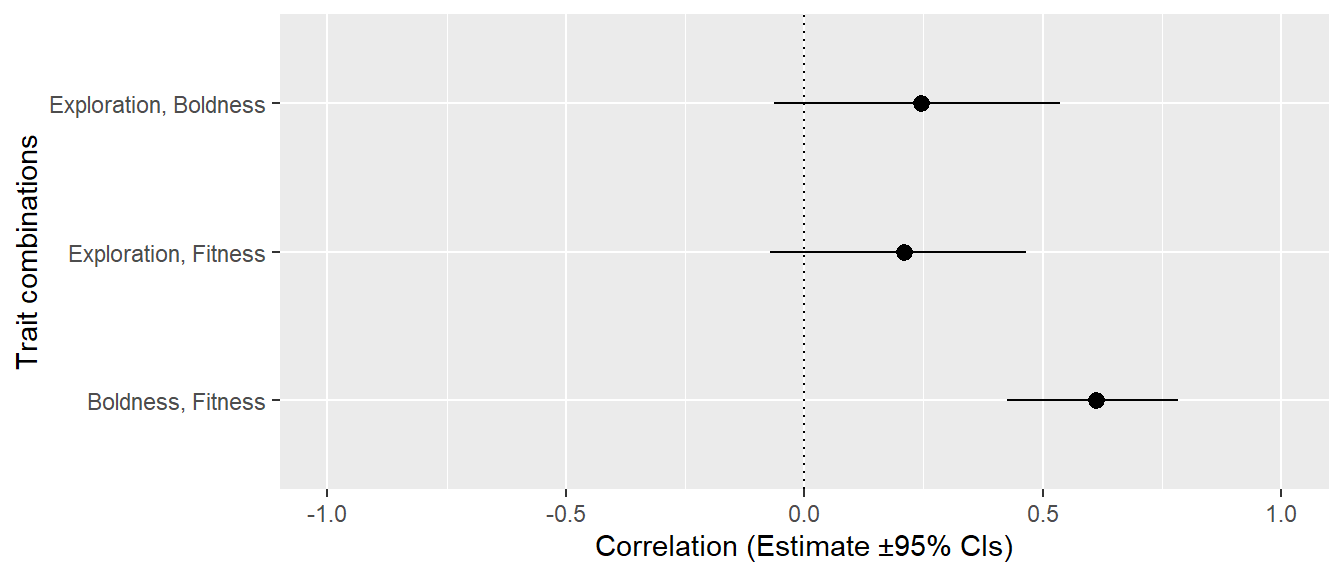

---

BLUPで散布図

ランダム効果のposterior modes (BLUPs from the MCMCglmm model) をFull-modelから抽出し、個性形質と適応度の関係を図示。図示のためにBLUPを使うのはOK

個性と適応度の個体毎の点推定を取り出す

ここではBoldnessー適応度の関連を調べる

df_bf_coefs <- data_frame(
  # Same as writing as: names(colMeans(mcmc_E_B_fit$Sol))
  Trait = attr(colMeans(mcmc_E_B_fit$Sol), "names"),
  # $Solには１属性当たり４つの値が格納されている。なんだこれは？
  # ここではcoMeansで4つの値の平均を取って今後の分析に使う
  Value = colMeans(mcmc_E_B_fit$Sol)
  ) %>%
  # この時点では全ての項目の推定値がまぜこぜに1列に並んでいる
  # BLUPは例えば以下のように格納されている：　traitexploration.ID.S_1
  # これを"."で分割
  separate(Trait, c("Trait","Type","ID"), sep = "\\.", fill = "right") %>%
  filter(
    # ID列に値があるのは個体毎の推定値だけ。これを取り出す
    Type == "ID",
    # ここではboldnessと、相対適応度を取り出す
    Trait %in% c("traitboldness", "traitrel_fitness")
    ) %>%
  select(-Type) %>%
  pivot_wider(names_from = Trait, values_from = Value)

回帰直線を得る

• Boldnessに対する相対適応度を傾き
  • \(\frac{boldnessと相対適応度の共分散}{boldnessの分散}\)

B_fit_slope <- mcmc_E_B_fit$VCV[,"traitrel_fitness:traitboldness.ID"]/
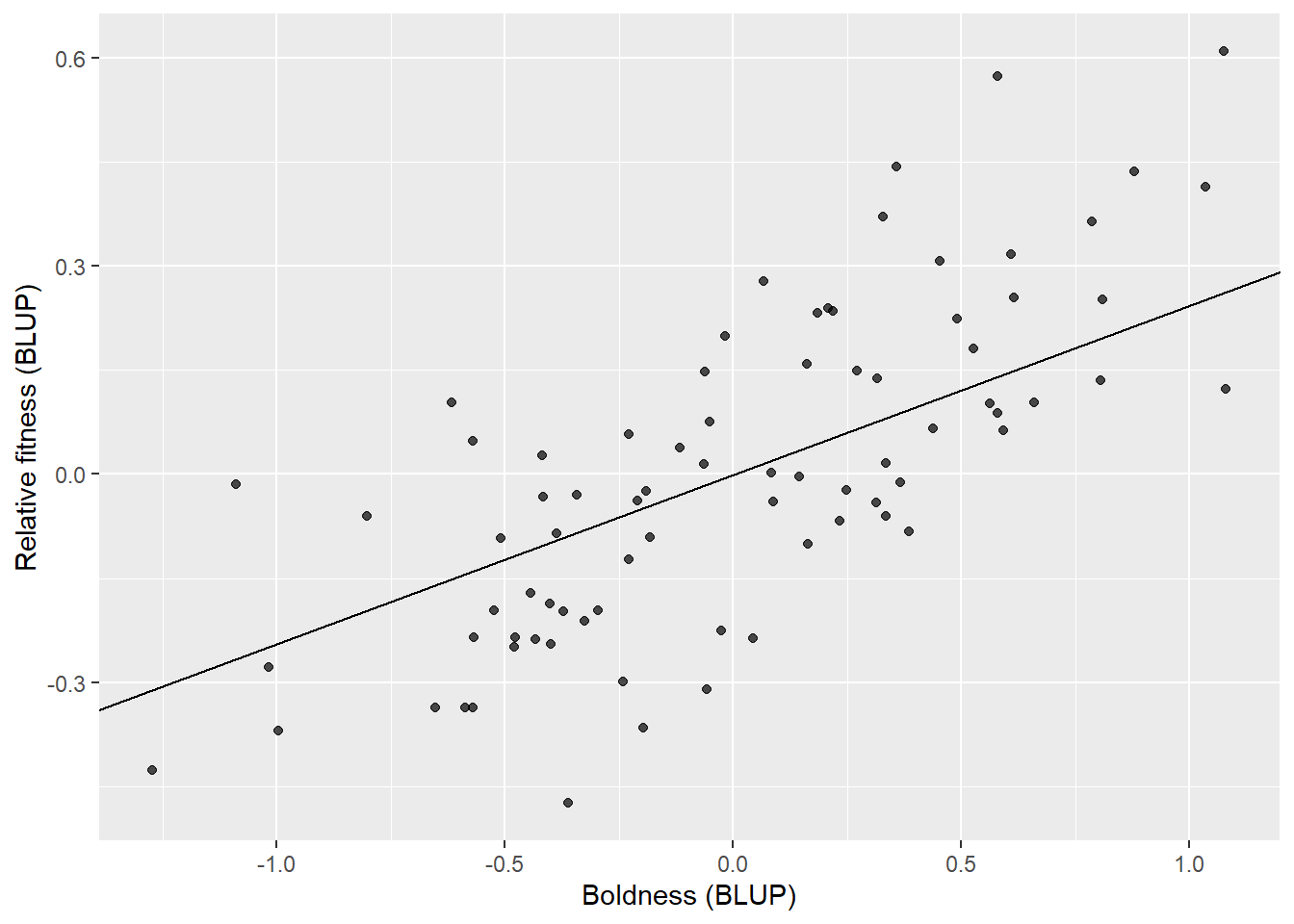
  mcmc_E_B_fit$VCV[,"traitboldness:traitboldness.ID"]

図示

ggplot(df_bf_coefs, aes(x = traitboldness, y = traitrel_fitness, group = ID)) +
  geom_point(alpha = 0.7) +
  geom_abline(intercept = 0, slope = mean(B_fit_slope)) +
  labs(
    x = "Boldness (BLUP)",
    y = "Relative fitness (BLUP)"
    )

---

brms : Mitchell et al

David Mitchell, Christa Beckmann, Peter A Biro: Supplement

brmsとは

概要: Bürkner 2017

• Bayesian multilevel modelを扱う
• Stan, C++を経由

MCMCglmmとの比較

1. 〇複数のマルコフ連鎖を走らせれる
2. 〇共分散の事前分布が柔軟に指定できる
3. 〇Link関数が柔軟
4. 〇Robust linear modelsができる

など。利点はそれなりに多いが（特に①）、問題はそれを扱えるか…。

まあMCMCglmmでいいか。

---

ASReml-R

Avoid this because it’s not free